Kannst du mir sagen wie ich das ablesen kann?
Ich muss alle Punkte bekommen, sonst bin ich nicht durch

ich stell mal alles rein und versuch dann die sachen zu machen, dich ich kann, aber das mit dem Ablesen, pff keine ahnung..
Frage 1 1 Punkte
Speichern Der durchschnittliche Bestand an Wildlachs liegt bei 1.000.000 (Nullhypothese mu= 1.000.000, Alternativhypothese mu≠ 1.000.000), wobei von einer Abweichung von +/- 250.000 Tieren ausgegangen wird (Standardabweichung=250.000). Aufgrund der Überfischung wird wöchentlich der Bestand überprüft. Sie betrachten die Ergebnisse der letzten 100 Tage. Sie testen nun ob sich der Fischbestand signifikant geändert hat, wenn das Signifikanzniveau bei 0.05 liegt. (Normalverteilt)
Wie groß müssen sie den Stichprobenumfang mindestens wählen damit die Power des Tests im Fall mu=950.000 mindestens 65% beträgt (dimensionslos, in ganzen Zahlen)? Verwenden Sie zur Beantwortung der Frage die folgenden 4 Gütefunktionen (n ist entweder 80, 100, 120 oder 150).



Frage 2 1 Punkte
Speichern In einer Fabrik werden Messbecher hergestellt, um die Qualität zu überprüfen, wird monatlich eine Stichprobe von 100 Messbechern von der Größe 1000ml (Nullhypothese mu = 1000) entnommen und auf eine mögliche Abweichung untersucht (Alternativhypothese mu ≠ 1000). Das Unternehmen testet bei einem Signifikanzniveau von 0.02. (Standardabweichung von 0.20 ml)
Bestimmen Sie anhand der Gütefunktion für mu=1000.03 die Wahrscheinlichkeit für den Fehler 2. Art (dimensionslos und auf zwei Dezimalstelle runden)!



Frage 3 1 Punkte
Speichern
Bei einem Wasserfall in Tirol stürzen täglich durchschnittlich 1 000 000 Liter Wasser die Fälle hinunter. Es kann angenommen werden, dass die Wassermenge normalverteilt ist mit einer Standardabweichung von 85 000 Litern.
Aufgrund der großen Wassermenge und einer Fallhöhe von ca. 400 m wurde dort vor zwei Jahren ein Speicherkraftwerk errichtet. Während des Jahres unterliegt die zufließende Wassermenge großen Schwankungen, vor allem in den Sommermonaten. Daher muss der Wasserdurchfluss laufend überwacht werden. In den letzten 60 Tagen wurde ein durchschnittlicher Wasserdurchfluss von 980 000 Litern gemessen. Testen Sie nun anhand eines Konfidenzintervalls zum Signifikanzniveau von 0.05, ob es sich um eine signifikante Abweichung handelt.  H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [961 949.77, 998 050.23], H0 wird beibehalten
Mit diesen Angaben nicht berechenbar.
H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [958 492.03, 1 001 507.97], H0 wird abgelehnt
H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [958 492.03, 1 001 507.97], H0 wird beibehalten
H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [961 949.77, 998 050.23], H0 wird abgelehnt
H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [961 949.77, 998 050.23], H0 wird beibehalten
Mit diesen Angaben nicht berechenbar.
H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [958 492.03, 1 001 507.97], H0 wird abgelehnt
H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [958 492.03, 1 001 507.97], H0 wird beibehalten
H0: µ = 1 000 000 gegen H1: µ ≠ 1 000 000, Konfidenzintervall [961 949.77, 998 050.23], H0 wird abgelehnt

Frage 4 1 Punkte
Speichern Ein Student trinkt regelmäßig vor den Lehrveranstaltungen Kaffee, den er immer vom selben Kaffeeautomaten entnimmt. Er hat jedoch das Gefühl, dass in seinem Becher immer zu wenig abgefüllt ist. Er wendet sich deshalb an den Automatenbetreiber, der ihm eine Füllmenge von 190 ml bei einer Standardabweichung von 12 ml garantiert, wobei davon auszugehen ist, dass die Füllmenge normalverteilt ist. Der Student will es genau wissen und bestimmt für sieben zufällig und unabhängig voneinander ausgewählte Kaffeebecher die durchschnittliche Füllmenge von 183.14 ml. Prüfen Sie zum Signifikanzniveau von 10%, ob der Student mit seiner Vermutung richtig liegt.
 H0:µ≥190 gegen H1:µ<190; Der Wert der Teststatistik ist -1.5125, der kritische Wert beträgt -1.2816, H0 ist daher abzulehnen.
H0:µ≥190 gegen H1:µ<190; Der Wert der Teststatistik ist -1.5125, der kritische Wert beträgt -1.6449, H0 ist daher abzulehnen.
H0:µ≤190 gegen H1:µ>190; Der Wert der Teststatistik ist 1.4003, der kritische Wert beträgt 1.4398, H0 ist daher beizubehalten.
H0:µ≤190 gegen H1:µ>190; Der Wert der Teststatistik ist -1.4003, der kritische Wert beträgt 1.6449, H0 ist daher beizubehalten.
Mit diesen Angaben nicht berechenbar.
r.
H0:µ≥190 gegen H1:µ<190; Der Wert der Teststatistik ist -1.5125, der kritische Wert beträgt -1.2816, H0 ist daher abzulehnen.
H0:µ≥190 gegen H1:µ<190; Der Wert der Teststatistik ist -1.5125, der kritische Wert beträgt -1.6449, H0 ist daher abzulehnen.
H0:µ≤190 gegen H1:µ>190; Der Wert der Teststatistik ist 1.4003, der kritische Wert beträgt 1.4398, H0 ist daher beizubehalten.
H0:µ≤190 gegen H1:µ>190; Der Wert der Teststatistik ist -1.4003, der kritische Wert beträgt 1.6449, H0 ist daher beizubehalten.
Mit diesen Angaben nicht berechenbar.
r.






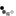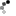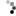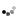
 Zitieren
Zitieren



Lesezeichen